Тема: Логические основы компьютера.

1. Основы логики.

Логика – наука о законах и формах мышления.

Высказывание (суждение) – некоторое предложение, которое может быть истинно (верно) или ложно.

Утверждение – суждение, которое требуется доказать или опровергнуть.

Рассуждение – цепочка высказываний или утверждений, определенным образом связанных друг с другом.

Умозаключение – логическая операция, в результате которой из одного или нескольких данных суждений получается (выводится) новое суждение.

Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных логическое выражение может принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0).

Сложное логическое выражение – логическое выражение, составленное из одного или нескольких простых (или сложных) логических выражений, связанных с помощью логических операций. 

2. Логические элементы компьютера. Схемы логических элементов и их таблицы истинности.

Как при строительстве дома применяют различного рода типовые блоки – кирпичи, рамы, двери и т.п., так и при разработке компьютера используют типовые электронные схемы. Каждая схема состоит из определенного набора типовых электронных элементов.

Электронным элементом называется соединение различных деталей, в первую очередь – диодов и транзисторов, а также резисторов и конденсаторов, в виде электрической схемы, выполняющей некоторую простейшую функцию.

Электронный элемент, реализующий логическую функцию, называется логическим элементом.

Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарную логическую функцию.

Тысячи микроскопических электронных переключателей в кристалле интегральной схемы сгруппированы в системы, выполняющие логические операции, т.е. операции с предсказуемыми результатами, и арифметические операции над двоичными числами. Соединенные в различные комбинации, логические элементы дают возможность компьютеру решать задачи, используя язык двоичных кодов.

Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и др. (называемые также вентилями), а также триггер, регистр, сумматор.

Триггер – это логическая схема, способная сохранять одно из двух состояний до подачи нового сигнала на вход. Это, по сути, разряд памяти, способный хранить 1 бит информации.

Регистр – это устройство, состоящее из последовательности триггеров. Регистр предназначен для хранения многоразрядного двоичного числового кода, которым можно представлять и адрес, и команду, и данные.

Сумматор – это устройство, предназначенное для суммирования двоичных кодов.

С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.

Чтобы представить два логических состояния «1» и «0» в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт.

Высокий уровень обычно соответствует значению «истина» («1»), а низкий – значение «ложь («0»).

Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.

Работу логических элементов описывают с помощью таблиц истинности.

Таблица истинности – это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значениями истинности выходного сигнала (результата операции) для каждого из этих сочетаний.

Логические операции и таблицы истинности

Табл. 9. Логическое умножение 

A	B	F
1	1	1
1	0	0
0	1	0
0	0	0

 

 

 

 

 

 

 

F = A & B.

Логическое умножение КОНЪЮНКЦИЯ - это новое сложное выражение будет истинным только тогда, когда истинны оба исходных простых выражения. Конъюнкция определяет соединение двух логических выражений с помощью союза И.

 

 Табл.10. Логическое сложение

A	B	F
1	1	1
1	0	1
0	1	1
0	0	0

 

 

 

 

 

 

F = A + B 

Логическое сложение – ДИЗЪЮНКЦИЯ - это новое сложное выражение будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) выражений. Дизъюнкция определяет соединение двух логических выражений с помощью союза ИЛИ.

Табл.11. Инверсия

A	неА
1	1
1	0

 

 

 

 

Логическое отрицание: ИНВЕРСИЯ - если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным/ Данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО

 

 Табл.12. Импликация

A	B	F
1	1	1
1	0	0
0	1	1
0	0	1

 

 

 

 

 

 

Логическое следование: ИМПЛИКАЦИЯ - связывает два простых логических выражения, из которых первое является условием (А), а второе (В)– следствием из этого условия. Результатом ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно. Обозначается символом "следовательно"  и  выражается словами ЕСЛИ … , ТО …

Порядок выполнения логических операций в сложном логическом выражении:

1. инверсия

2. конъюнкция

3. дизъюнкция

4. импликация

5. эквивалентность

3. Электронно-логические схемы триггера и сумматора.

Триггер – это электронная схема, широко применяемая в регистрах компьютера для надежного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое – двоичному нулю.

Термин «триггер» происходит от английского слова trigger – защелка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip – flop, что в переводе означает «хлопанье». Это звукоподражательное название электронной схемы указывает на ее способность почти мгновенно переходить из одного электрического состояния в другое и наоборот.

Самый распространенный тип триггера – так называемый RS – триггер ( S и R соответственно от английских слов set – установка и reset – сброс). Условное обозначение триггера – на рис.5. Он имеет два симметричных входа S и R и два симметричных выхода Q и  , причем выходной сигнал Q является логическим отрицанием сигнала  . На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов. Наличие импульса на входе будем считать единицей, а его отсутствие – нулем.

Рис. 5. Реализация триггера с помощью вентилей ИЛИ-НЕ

 

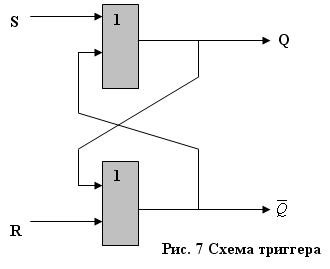
Табл.13. Реализация триггера с помощью вентилей ИЛИ-НЕ

S	R	Q
0	0	Запрещено
0	1	1	0
1	0	0	1
1	1	Хранение бита

Проанализируем возможные комбинации значений входов R и S триггера, используя его схему и таблицу истинности схемы ИЛИ-НЕ (см. табл. 13).

1.                  Если на входы триггера подать S = «1», R = «0», то (независимо от состояния) на выходе Q верхнего вентиля появится «0». После этого на входах нижнего вентиля окажется R = «0», Q = «0» и выход   станет равным «1».

2.                  Точно так же при подаче «0» на вход S и «1» на вход R на выходе   появится «0», а на Q – «1».

3.                  Если на входы S и R подана логическая «1», то состояние Q и   не меняется.

4.                  Подача на оба входа R и S логического «0» может привести к неоднозначному результату, поэтому эта комбинация входных сигналов запрещена.

Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта соответственно 8*2¹⁰=8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.

 

Сумматор - это электронная логическая схема,выполняющая суммирование двоичных чисел.  Сумматор служит прежде всего центральным узлом арифметико–логического устройства компьютера, однако он находит применение также и в других устройствах машины.

Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров, с рассмотрения которых мы и начнем. Условное обозначение одноразрядного сумматора приведено на рис. 8.

Одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами, работа которого может быть описана следующей таблицей истинности – табл.14.

Табл. 14. Схема полусумматора.

 

Входы			Выходы
Первое слагаемое	Второе слагаемое	Перенос	Сумма	Перенос
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Если требуется складывать двоичные слова длиной два и более бит, то можно использовать последовательное соединение таких сумматоров, причем для двух соседних сумматоров выход переноса одного сумматора является входом для другого.